METODOLOGIA DA MATEMÁTICA
Dois automóveis estão indo de A para B.
Observe o percurso que cada uma fez e responda a pergunta assinalando a alternativa correta.
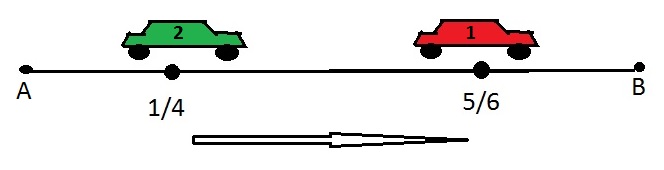
Qual a diferença entre o percurso do carro 1 e do carro 2?
7/12
4/2
4/6
4/12
6/10
No primeiro ano entre as operações de subtração, devem ser incluídas subtrações de mais de um subtraendo e também subtraendos iguais (ROSA, p.121. 2010). Em seguida fazer a ação de dividir. Ex: Uma criança tem em mãos 8 lápis, o professor solicita que divida estes lápis com 3 colegas.
Com base nos estudos acerca da divisão leia e analise as alternativas abaixo, e, em seguida assinale a única alternativa que não confere com o estudado.
A ideia de repartir na divisão é utilizada quando queremos determinar o número de elementos de cada agrupamento e o número de elementos que resta, caso a divisão não seja exata.
Chama-se divisão a operação que entre dois números naturais, nos fornece um terceiro número, que indica quantas vezes o primeiro contém o segundo.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é desconhecido e precisamos determinar quantos agrupamentos serão necessários.
Ao dividir em partes iguais utilizamos as ideias de repartir e medir.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão necessários.
Com o auxílio do material dourado, a professora X apresentou aos alunos a quantidade abaixo:

Em seguida solicitou que dividissem em 6 partes iguais.
O resultado foi:
Os alunos tiveram que decompor a centena em dezenas em seguida juntaram às dezenas que já tinham.
Dividiram as dezenas.
O resultado foi decomposto em unidades e acrescido as unidades já existentes.
Dividiram as unidades. O resultado foi: duas dezenas e três unidades.
Assinale a alternativa que não confere com o estudado.
Esta divisão poderia ser feita sem o material concreto. Neste caso, a decomposição das centenas e das dezenas seria feita mentalmente, apenas representada.
A centena foi decomposta, porque só havia uma, e, neste caso, não daria para dividir em seis.
Para realizar a divisão, solicitada pela professora, não seria necessário todo processo de decomposição, isso porque, o número representado no material dourado é bem maior que seis.
Os alunos poderiam decompor a centena e as dezenas em unidades, e, depois juntar as unidades já existentes, que o resultado da divisão não alteraria.
Não seria possível dividir as unidades já existentes, em quantidades exatas, sem que as dezenas restantes fossem decompostas e acrescidas a elas.
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.
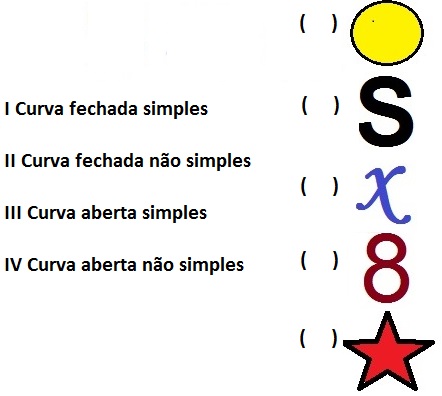
É correto apenas o que se afirma em:
I, III, IV, II, I
I, II, II, IV, I
I, III, IV, I, II
I, IV, III, II, I
I, II, IV, III, I
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
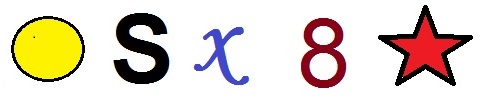
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.
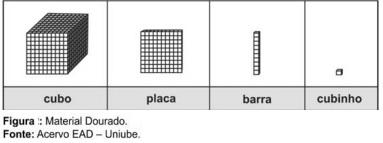
Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.
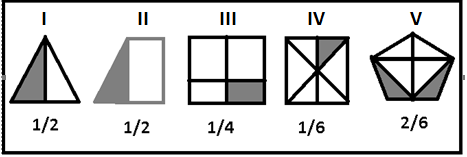

7/12
4/2
4/6
4/12
6/10
No primeiro ano entre as operações de subtração, devem ser incluídas subtrações de mais de um subtraendo e também subtraendos iguais (ROSA, p.121. 2010). Em seguida fazer a ação de dividir. Ex: Uma criança tem em mãos 8 lápis, o professor solicita que divida estes lápis com 3 colegas.
Com base nos estudos acerca da divisão leia e analise as alternativas abaixo, e, em seguida assinale a única alternativa que não confere com o estudado.
A ideia de repartir na divisão é utilizada quando queremos determinar o número de elementos de cada agrupamento e o número de elementos que resta, caso a divisão não seja exata.
Chama-se divisão a operação que entre dois números naturais, nos fornece um terceiro número, que indica quantas vezes o primeiro contém o segundo.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é desconhecido e precisamos determinar quantos agrupamentos serão necessários.
Ao dividir em partes iguais utilizamos as ideias de repartir e medir.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão necessários.
Com o auxílio do material dourado, a professora X apresentou aos alunos a quantidade abaixo:

Em seguida solicitou que dividissem em 6 partes iguais.
O resultado foi:
Os alunos tiveram que decompor a centena em dezenas em seguida juntaram às dezenas que já tinham.
Dividiram as dezenas.
O resultado foi decomposto em unidades e acrescido as unidades já existentes.
Dividiram as unidades. O resultado foi: duas dezenas e três unidades.
Assinale a alternativa que não confere com o estudado.
Esta divisão poderia ser feita sem o material concreto. Neste caso, a decomposição das centenas e das dezenas seria feita mentalmente, apenas representada.
A centena foi decomposta, porque só havia uma, e, neste caso, não daria para dividir em seis.
Para realizar a divisão, solicitada pela professora, não seria necessário todo processo de decomposição, isso porque, o número representado no material dourado é bem maior que seis.
Os alunos poderiam decompor a centena e as dezenas em unidades, e, depois juntar as unidades já existentes, que o resultado da divisão não alteraria.
Não seria possível dividir as unidades já existentes, em quantidades exatas, sem que as dezenas restantes fossem decompostas e acrescidas a elas.
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.

É correto apenas o que se afirma em:
I, III, IV, II, I
I, II, II, IV, I
I, III, IV, I, II
I, IV, III, II, I
I, II, IV, III, I
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
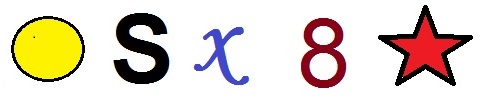
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

A ideia de repartir na divisão é utilizada quando queremos determinar o número de elementos de cada agrupamento e o número de elementos que resta, caso a divisão não seja exata.
Chama-se divisão a operação que entre dois números naturais, nos fornece um terceiro número, que indica quantas vezes o primeiro contém o segundo.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é desconhecido e precisamos determinar quantos agrupamentos serão necessários.
Ao dividir em partes iguais utilizamos as ideias de repartir e medir.
A ideia de medida é utilizada quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão necessários.
Com o auxílio do material dourado, a professora X apresentou aos alunos a quantidade abaixo:

Em seguida solicitou que dividissem em 6 partes iguais.
O resultado foi:
Os alunos tiveram que decompor a centena em dezenas em seguida juntaram às dezenas que já tinham.
Dividiram as dezenas.
O resultado foi decomposto em unidades e acrescido as unidades já existentes.
Dividiram as unidades. O resultado foi: duas dezenas e três unidades.
Assinale a alternativa que não confere com o estudado.
Esta divisão poderia ser feita sem o material concreto. Neste caso, a decomposição das centenas e das dezenas seria feita mentalmente, apenas representada.
A centena foi decomposta, porque só havia uma, e, neste caso, não daria para dividir em seis.
Para realizar a divisão, solicitada pela professora, não seria necessário todo processo de decomposição, isso porque, o número representado no material dourado é bem maior que seis.
Os alunos poderiam decompor a centena e as dezenas em unidades, e, depois juntar as unidades já existentes, que o resultado da divisão não alteraria.
Não seria possível dividir as unidades já existentes, em quantidades exatas, sem que as dezenas restantes fossem decompostas e acrescidas a elas.
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.

É correto apenas o que se afirma em:
I, III, IV, II, I
I, II, II, IV, I
I, III, IV, I, II
I, IV, III, II, I
I, II, IV, III, I
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
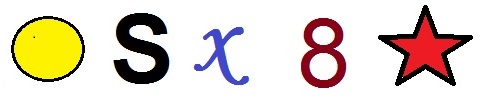
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.


Esta divisão poderia ser feita sem o material concreto. Neste caso, a decomposição das centenas e das dezenas seria feita mentalmente, apenas representada.
A centena foi decomposta, porque só havia uma, e, neste caso, não daria para dividir em seis.
Para realizar a divisão, solicitada pela professora, não seria necessário todo processo de decomposição, isso porque, o número representado no material dourado é bem maior que seis.
Os alunos poderiam decompor a centena e as dezenas em unidades, e, depois juntar as unidades já existentes, que o resultado da divisão não alteraria.
Não seria possível dividir as unidades já existentes, em quantidades exatas, sem que as dezenas restantes fossem decompostas e acrescidas a elas.
As formas geométricas estão por toda parte, na natureza, no nosso dia a dia, no nosso corpo, nas letras, nos números. E essas formas são compostas por segmentos ininterruptos, podendo ser retos ou curvos. Geometricamente falando, esses segmentos são chamados de CURVAS. Assim, as curvas são segmentos interruptos; não necessariamente retos. Dessa forma, temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente ditas.
Com base neste estudo analise as curvas abaixo, em seguida, numere a segunda coluna de acordo com a primeira.

É correto apenas o que se afirma em:
I, III, IV, II, I
I, II, II, IV, I
I, III, IV, I, II
I, IV, III, II, I
I, II, IV, III, I
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
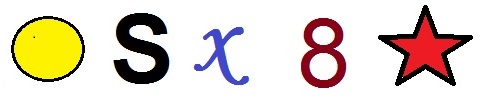
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.


I, III, IV, II, I
I, II, II, IV, I
I, III, IV, I, II
I, IV, III, II, I
I, II, IV, III, I
Sobre as CURVAS, leu-se que elas estão em todas as partes. No nosso corpo; na natureza quando olhamos uma montanha, um rio; no nosso alfabeto e nos algarismos. Podemos dizer as curvas são segmentos interruptos; não necessariamente retos. Assim, podemos dizer que temos segmentos retilíneos a que chamamos de reta; e segmentos curvilíneos, que são as curvas propriamente dita.
As curvas podem ser; abertas simples, que não se cruzam; abertas não simples, que tem um ponto de encontro e apenas fechadas.
Com base neste estudo analise as curvas abaixo, em seguida, assinale a sequência que apresenta as nomenclaturas corretas.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada não simples, curva fechada simples.
Curva fechada, curva aberta simples, curva aberta simples, curva fechada, curva aberta simples.
Curva fechada, curva aberta simples, curva aberta não simples, curva fechada, curva aberta não simples.
Curva fechada, curva aberta não simples, curva aberta não simples, curva fechada, curva aberta não simples.
I - A partir do momento em que o homem abstraiu a ideia de número e a sua vida social foi se intensificando, houve a necessidade de contar conjuntos cada vez mais numerosos.
Porque:
II- Quando precisamos contar uma grande quantidade de coisas, separando os objetos em grupos, isso facilita a contagem, o que implica muitas situações. Os agrupamentos são necessários para facilitar o trabalho do homem.
A respeito dessas asserções, assinale a opção correta.
As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

As asserções I e II são proposições verdadeiras, e a II é justificativa da I.
As asserções I e II são proposições falsas.
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
As asserções I e II são proposições verdadeiras, mas a II não é justificativa da I.
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.


V, V, F, V, F
V, F, V, V, V
V, V, F, F, V
V, V, V, F, F
V, V, V, V, V
O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:
Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.
As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.
Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.
As frações 3/6, 6/12, e 1/2 são equivalentes.
Com base nos elementos fundamentais da geometria, analise as alternativas abaixo que exemplificam a ideia de: ponto, reta e plano.
A cabeça de um alfinete.
O piso da sala de aula.
Uma corda de violão bem esticada.
As estrelas no céu.
Um campo de futebol.
Assinale a sequência correta.
Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

Plano, ponto, reta, ponto e reta.
Ponto, plano, reta, plano e reta.
Ponto, plano, reta, ponto e plano.
Ponto, reta, reta, ponto e plano.
Ponto, plano, plano, ponto e reta.
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.

